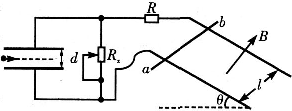
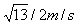如图所示,质量为M的导体棒ab,垂直放在相距为l 的平行光滑金属导轨上,导轨平面与水平面的夹角为θ,并处于磁感应强度大小为B方向垂直于导轨平面向上的匀强磁场中,左侧是水平放置间距为d的平行金属板,R和Rx分别表示定值电阻和滑动变阻器的阻值,不计其他电阻.
(1)调节Rx=R,释放导体棒,当棒沿导轨匀速下滑时,求通过棒的电流I及棒的速率v.
(2)改变Rx,待棒沿导轨再次匀速下滑后,将质量为m带电量为+q的微粒水平射入金属板间,若它能匀速通过,求此时的Rx.
(1)导体棒匀速下滑时,Mgsinθ=BIl①
I=
②Mgsinθ Bl
设导体棒产生的感应电动势为E0
E0=BLv③
由闭合电路欧姆定律得:
I=
④E0 R+Rx
联立②③④,得
v=
⑤2MgRsinθ B2l2
(2)改变Rx由②式可知电流不变.设带电微粒在金属板间匀速通过时,板间电压为U,电场强度大小为E
U=IRx⑥
E=
⑦U d
mg=qE⑧
联立②⑥⑦⑧,得
Rx=
⑨mBld qMsinθ
答:(1)通过棒的电I=
及棒的速率v=Mgsinθ Bl
.Mgsinθ Bl
(2)此时的Rx=Mgsinθ Bl