问题
问答题
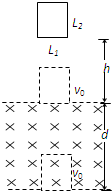
如图所示,水平的平行虚线间距为d,其间有磁感应强度为B的匀强磁场.一个长方形线圈的边长分别为L1、L2,且L2<d,线圈质量m,电阻为R.现将线圈由静止释放,测得当线圈的下边缘到磁场上边缘的距离为h时,其下边缘刚进入磁场和下边缘刚穿出磁场时的速度恰好相等.求:
(1)线圈刚进入磁场时的感应电流的大小;
(2)线圈从下边缘刚进磁场到下边缘刚出磁场(图中两虚线框所示位置)的过程做何种运动,求出该过程最小速度v;
(3)线圈进出磁场的全过程中产生的总焦耳热Q总.
答案
(1)根据机械能守恒得
mgh=
m1 2
,得v0=v 20 2gh
感应电动势 E=BL1v0,
由闭合电路欧姆定律得 I=
=E R
.BL1 2gh R
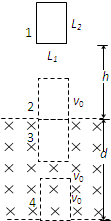
(2)线框进入磁场的过程做加速度减小的减速运动,完全进入磁场后做加速度为g的匀加速运动,则知3位置时线圈速度最小,则有
-v2=2g(d-L2),v 20
得v=2g(h+L2-d)
(3)由于线圈完全处于磁场中时不产生电热,线圈进入磁场过程中产生的电热Q就是线圈从图中2位置到4位置产生的电热,而2、4位置动能相同.
由能量守恒Q=mgd
由对称性可知:Q总=2Q=2mgd
答:
(1)线圈刚进入磁场时的感应电流的大小是
;BL1 2gh R
(2)线圈从下边缘刚进磁场到下边缘刚出磁场的过程中最小速度v是
;2gh(h+L2-d)
(3)线圈进出磁场的全过程中产生的总焦耳热Q总是2mgd.
