如图(甲)所示,一对足够长平行光滑轨道放置在水平面上,两轨道间距l=0.5m,左侧接一阻值为R=1的电阻;有一金属棒静止地放在轨道上,与两轨道垂直,金属棒及轨道的电阻皆可忽略不计,整个装置处于垂直轨道平面竖直向下的匀强磁场中.t=0时,用一外力F沿轨道方向拉金属棒,使棒以加速度a=0.2m/s2做匀加速运动,外力F与时间t的关系如图(乙)所示.
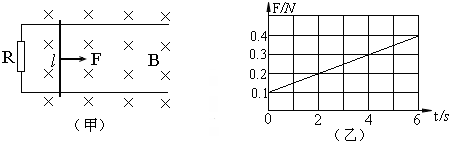
(1)求金属棒的质量m
(2)求磁感强度B
(3)当力F达到某一值时,保持F不再变化,金属棒继续运动3秒钟,速度达到1.6m/s且不再变化,测得在这3秒内金属棒的位移s=4.7m,求这段时间内电阻R消耗的电能.
由图(乙)知F=0.1+0.05t
(1)F合=F-F安=(0.1+0.05t)-
=ma,B2l2v R
考虑t=0时,v=at=0
即 F合=0.1N
牛顿第二定律得:m=
=F合 a
kg=0.5kg0.1 0.2
(2)棒做匀加速运动,
F合=(0.1+0.05t)-
=0.1+(0.05-B2l2at R
)t=常数B2l2a R
所以0.05-
=0,B2l2a R
解得:B=
=0.05R l2a
=1T0.05×1 0.52×0.2
(3)F变为恒力后,金属棒做加速度逐渐减小的变加速运动,经过3秒钟,速度达到最大vm=1.6m/s,此后金属棒做匀速运动.
vm=1.6m/s时,F安=0
F=F安=
=B2l2vm R
N=0.4N,12×0.52×1.6 1
将F=0.4N代入F=0.1+0.05t,求出变加速运动的起始时间为:t=6s,
该时刻金属棒的速度为:v6=at═0.2×6=1.2m/s;
这段时间内电阻R消耗的电能:E=WF-△Ek=FS-
m(1 2
-v 2m
)=0.4×4.7-v 26
×0.5(1.62-1.22)=1.6J1 2
答:(1)则金属棒的质量0.5kg;
(2)则磁感强度1T;
(3)当力F达到某一值时,保持F不再变化,金属棒继续运动3秒钟,速度达到1.6m/s且不再变化,测得在这3秒内金属棒的位移s=4.7m,则这段时间内电阻R消耗的电能为1.6J.
