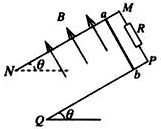
如图所示,足够长的光滑平行金属导轨MN、PQ与水平面成θ=30°角放置,一个磁感应强度B=1.00T的匀强磁场垂直穿过导轨平面,导轨上端M与P间连接阻值为R=0.30Ω的电阻,长L=0.40m、电阻r=0.10Ω的金属棒ab与MP等宽紧贴在导轨上,现使金属棒ab由静止开始下滑,其下滑距离与时间的关系如下表所示,导轨电阻不计,g=10m/s2
| 时间t(s) | 0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 |
| 下滑距离x(m) | 0 | 0.02 | 0.08 | 0.17 | 0.27 | 0.37 | 0.47 | 0.57 |
(2)金属棒的质量
(3)在0.7s时间内,整个回路产生的热量.
(1)根据法拉第电磁感应定律得:感应电动势的平均值
=. E
=△Φ △t BL•x △t
感应电流的平均值
=. I . E r+R
电荷量 q=
•△t=. I BLx R+r
由表中数据可知 x=0.27m
∴q=
=BLx R+r
C=0.27C;1×0.4×0.27 0.3+0.1
(2)由表中数据可知,0.3s后棒作匀速运动的速度为:v=
=△x △t
=1m/s0.1 0.1
由mgsinθ-F=0;
安培力表达式:F=BIL;
由闭合电路欧姆定律得:I=
;E R+r
感应电动势为:E=BLv;
联立得,m=
=B2L2v (R+r)gsinθ
=0.08kg;12×0.42×1 0.4×10×sin30°
(3)棒在下滑过程中,有重力和安培力做功,克服安培力做的功等于回路的焦耳热.则:
mgsin30°•x7-Q=
mv2-01 2
得:Q=mgsin30°•x7-
mv2=0.08×10×0.57×0.5-1 2
×0.08×12=0.416J1 2
答:
(1)在0.4s时间内,通过金属棒ab截面的电荷量为0.27C.
(2)金属棒的质量为0.08C.
(3)在0.7s时间内,整个回路产生的热量为0.416J.
