问题
问答题
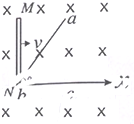
如图所示,光滑的金属框架abc固定在水平面内,顶角θ=53°,金属框架处在磁感应强度为B的匀强磁场中,磁场方向垂直水平面,t=0时,金属棒MN受向右的水平拉力F作用,从b点开始沿bc方向以速度v做匀速运动,在运动过程中MN始终垂直于bc,且与框架接触良好,框架bc边和金属棒MN单位长度的电阻均为r,框架ab边的电阻忽略不计(sin53°=0.8)
(1)求t时刻回路中的电流I;
(2)写出拉力F与杆的位移x的关系式,并类比v-t图象求位移的方法,写出拉力F做的功W与杆的位移x的关系式;
(3)求时间t内回路中产生的焦耳热Q.
答案
(1)金属棒的位移x=vt,
切割磁感线的有效长度:L=xtan53°=
x,4 3
感应电动势:E=BLv=
Bvx,4 3
回路总电阻:R=(x+
x)r=4 3
xr,7 3
回路电流:I=
,E R
解得:I=
;4Bv 7r
(2)导体棒受到的安培力:FB=BIL=
x,16B2v 21r
由平衡条件可得,外力F=FB=BIL=
x,16B2v 21r
外力的功:W=
Fx=1 2
x2;8B2v 21r
(3)克服安培力做功转化为焦耳热,
由能量守恒定律得:Q=W=
x2=8B2v 21r
t2;8B2v3 21r
答:(1)t时刻回路中的电流I=
;4Bv 7r
(2)拉力F与杆的位移x的关系式为:F=
x,拉力F做的功W与杆的位移x的关系式为W=16B2v 21r
x2;8B2v 21r
(3)时间t内回路中产生的焦耳热Q=
t2.8B2v3 21r
