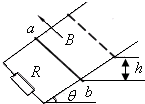
如图所示,两根金属导轨平行放置在倾角为θ=30°的斜面上,导轨左端接有电阻R=8Ω,导轨自身电阻不计.匀强磁场垂直于斜面向上,磁感应强度为B=0.5T.质量为m=0.1kg,电阻为r=2Ω的金属棒ab由静止释放,沿导轨下滑,如图所示.设导轨足够长,导轨宽度L=2m,金属棒ab下滑过程中始终与导轨接触良好,受到的摩擦阻力f=0.3N,当金属棒下滑的高度为h=3m时,恰好达到最大速度,g取10m/s2,求此过程中:
(1)金属棒的最大速度;
(2)电阻R中产生的热量;
(3)通过电阻R的电量.
(1)金属棒做匀速直线运动时,速度达到最大,设为v.
感应电动势:E=BLv,
电流:I=
,E R+r
安培力:F=BIL=
,B2L2v R+r
由平衡条件得:mgsinθ=F+f,
代入数据解得:v=2m/s;
(2)由能量守恒定律得:
mgh=Q+f•
+h sinθ
mv2,1 2
代入数据解得:Q=1J,
R上产生的热量:
QR=
Q=R R+r
×1=0.8J;8 8+2
(3)由法拉第电磁感应定律得:
E=
=△Φ △t
=B•S △t
,B•L• h sinθ R+r
电流:I=
,E R+r
电荷量:q=I△t,
代入数据解得:q=0.6C;
答:(1)金属棒的最大速度为2m/s;
(2)电阻R中产生的热量为0.8J;
(3)通过电阻R的电量为0.6C.

 之贻。(《静女》)
之贻。(《静女》)