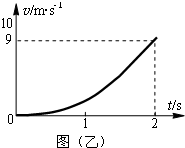
如图(甲)所示,足够长、电阻可以忽略的矩形金属框架abcd水平放置,ad与bc之间的距离为L=1m,左右两侧各连接一个定值电阻,阻值R1=R2=2.0Ω.垂直于框架固定一根质量m=0.2kg、电阻r=1.0Ω的金属棒ef,棒ef距离框架左侧s=0.5m.
(1)若在abfe区域存在竖直向上的均匀增强的匀强磁场,磁感应强度变化率
=0.2T/s,求电阻R1消耗的电功率.△B △t
(2)若金属棒ef处于竖直向上的匀强磁场中,磁感应强度B=2.0T,ef与导轨间的动摩擦因数μ=0.5.现使磁场以加速度a=5m/s2由静止开始向右匀加速运动,同时释放导体棒ef,则需要经过多长时间导体棒ef开始运动?(最大静摩擦力近似等于滑动摩擦力,ef始终处于磁场中)
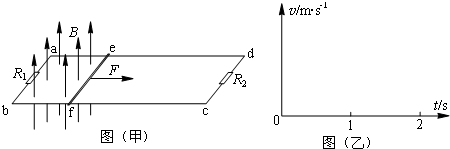
(3)上问中,从磁场开始运动计时起,在0~2s的时间内导体棒运动了7.5m的距离,电路中产生的焦耳热为2.9J(2s前导体棒运动状态已经稳定).求此过程中,运动磁场给系统提供的能量,并在图(乙)中定性画出导体棒的速度-时间图象.
(1)abfe回路产生的感应电动势为:
E=
=△Φ △t
Ls=0.2×1×0.5V=0.1V△B △t
总电阻为:R总=R1+
=2+R2r R2+r
=2×1 2+1
Ω,8 3
经过R1的电流为:I1=
=E R总
A=0.1 8 3
A=0.0375A3 80
电阻R1消耗的电功率为:P1=I12R1=0.03752×2W=2.8×10-3W
(2)导体棒ef刚要开始运动时,安培力与最大静摩擦力大小相等,即:BIefL=μmg
启动电流:Ief=
=μmg BL
A=0.5A0.5×0.2×10 2×1
总电阻为:R总′=r+
=1+R1R2 R1+R2
=2Ω2×2 2+2
此时电动势为:E′=IefR总′=0.5×2V=1V
而:E′=BLv1=BLat1,
解得:t1=
=E′ BLa
s=0.1s1 2×1×5
(3)ef棒开始运动后,水平方向受到两个力的作用,根据牛顿第二定律:
BIL-μmg=maef
即
(at-v磁)-μmg=maefB2L2 R′总
因此,棒开始运动后,做加速度增大的加速运动,
当aef=a=5m/s后运动状态稳定,磁场、ef棒的速度差值△v保持稳定,
△v=
=(μmg+ma)R′总 B2L2
m/s=1m/s(0.5×0.2×10+0.2×5)×2 22×12
2s时ef棒的速度为:vef=at-△v=5×2-1=9m/s
ef棒获得动能为:△Ek=
mvef2=1 2
×0.2×92J=8.1J1 2
2s内摩擦生热为:Q′=μmgs′=0.5×0.2×10×7.5J=7.5J
运动磁场给系统提供的能量为:E磁=△Ek+Q磁+Q′=8.1+2.9+7.5=18.5J
速度-时间图象如图所示.
答:(1)电阻R1消耗的电功率为2.8×10-3W.
(2)需要经过0.1s时间导体棒ef开始运动.
(3)此过程中,运动磁场给系统提供的能量为18.5J,速度-时间图象如图所示.