问题
实验题
( 8 分）某同学设想用如图甲的装置来测量滑块与导轨间的动摩擦因数。在气垫导轨上安装了两光电门l、2，滑块上固定一遮光条，滑块用细线绕过定滑轮与钩码相连。
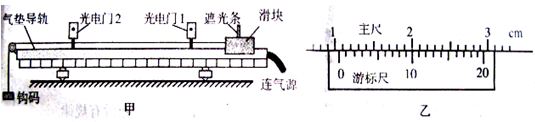
（1）用游标卡尺测光电门遮光条的宽度d，图乙中游标卡尺读数为 cm 。滑块在轨道上做匀变速运动时，先后通过光电门l 、2 所用的时间分别为t1、t2，两光电门间的距离为L ，用d 、t1、t2 、L 表示滑块运动的加速度a为
（2）要使细线中拉力近似等于钩码重力，滑块质量M 与钩码质量m 应满足 关系。
（3）满足（2）后，调整气垫导轨水平，断开气源时，测得滑块在轨道上运动的加速度为a1；不改变钩码的质量，接通气源，测得滑块在轨道上运动的加速度为a2，用“a1、a2、g来表示滑块与导轨间的动摩擦因数μ为 。
答案
⑴1.050；
；⑵M远大于m；⑶
。（每空2分）
题目分析：（1）通过图乙读改写即可，主尺是1cm，游标尺是10×0.05mm=0.50mm=0.050cm，故d=1.050cm；滑块在光电门1时的速度为v1=
，在光电门2时的速度为v2=
，故由公式v22－v12=2aL得，加速度a=；
（2）将M与m看成一个整体，应用牛顿第二定律可得：mg=(M+m)a，设细线中拉力为T，则再对钩码进行受力分析可得：mg－T=ma，联立以上两个式子解之得T=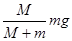
，故只有当M>>m时，T≈mg；
（3）断开气源时，mg－mgμ=(M+m)a1；接通气源时，mg=(M+m)a2；联立以上两式，解之得摩擦因数μ=。