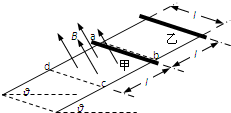
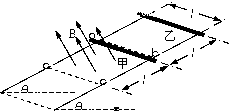
如图所示，电阻不计足够长的光滑平行金属导轨与水平面夹角θ=30

问题问答题

如图所示，电阻不计足够长的光滑平行金属导轨与水平面夹角θ=30°，导轨间距l，所在平面的正方形区域abcd内存在有界匀强磁场，磁感应强度为B=0.2T，方向垂直斜面向上．甲、乙金属杆质量均为m=0.02kg、电阻相同，甲金属杆处在磁场的上边界，乙金属杆距甲也为l，其中l=0.4m．同时无初速释放两金属杆，此刻在甲金属杆上施加一个沿着导轨的外力F，保持甲金属杆在运动过程中始终与乙金属杆未进入磁场时的加速度相同．且乙金属杆进入磁场后恰能做匀速直线运动，（取g=10m/s²）

（1）计算乙的电阻R．

（2）以刚释放两杆时作为零时刻，写出从开始到甲金属杆离开磁场的过程中，外力F随时间t的变化关系，并说明F的方向．

（3）若从开始释放到乙金属杆离开磁场，乙金属杆中 * * 生热量Q=

J，试求此过程中外力F对甲做的功．

答案

（1）甲乙加速度相同（5m/s²），当乙进入磁场时，甲刚出磁场；乙进入磁场时速度为：

2glsinθ

2×10×0.4×sin30°

m/s=2m/s

乙在磁场中匀速运动，有：mgsinθ=F=

B2l2v

得：R=

B2l2v

2mgsinθ

0．22×0．42×2

2×0.02×10×

Ω=0.064Ω

（2）甲在磁场中运动时，有：v=at=5t

根据牛顿第二定律得：

F+mgsin30°-F_A=ma

由于 a=gsin30°

外力F始终等于安培力，得：F=F_A=IlB=

Blv

lB=0.25t

F的方向沿导轨向下．

（3）乙进入磁场前，甲乙发出相同热量，设为Q₁，此过程中甲一直在磁场中，外力F始终等于安培力，则有：W_F=W_安=2Q₁，

乙在磁场中运动发出热量Q₂，利用动能定理有：mglsinθ-2Q₂=0

得：Q₂=0.02J

甲乙发出相同热量，有：Q₁=

Q-Q2

=0.0133J

由于甲出磁场以后，外力F为零．

得：W_F=2Q₁=

=0.0266J

答：（1）乙的电阻R为0.064Ω．

（2）从开始到甲金属杆离开磁场的过程中，外力F随时间t的变化关系为F=0.25t，F的方向沿导轨向下．

（3）此过程中外力F对甲做的功为0.0266J．