如图,相距L=1m、电阻不计的平行光滑长金属导轨固定在绝缘水平面上,两导轨左端间接有阻值R=2Ω的电阻,导轨所在足够长区域内加上与导轨所在平面垂直的匀强磁场,磁感应强度大小B=1T.现有电阻r=1Ω,质量m=1kg的导体棒ab垂直导轨放置且接触良好,当导体棒ab以速度v=12m/s从边界MN进入磁场后.
(1)求棒ab刚进入磁场时的加速度大小;
(2)棒ab进入磁场一段距离后,速度大小变为6m/s,求从进入磁场到此时的过程中电阻R产生的焦耳热为多少;
(3)求棒ab最终停的位置.
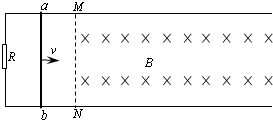
(1)当导体棒进入磁场切割磁感线时,导体棒受到的安培力:
F=BIL=
,B2L2v R+r
由牛顿第二定律得:
=maB2L2v R+r
代入数据解得:a=4m/s2;
(2)对导体棒,由能量守恒定律得:
mv2=1 2
mv′2+Q,1 2
在闭合电路中:Qr QR
=I2r I2R
=r R
,1 2
电路中的总热量;Q=Qr+QR,
代入数据解得:QR=36J;
(3)在导体棒运动的极短时间△t内,从t→△t时间内,多导体棒,由动量定理得:
-F△t=m△v,
安培力:F=
,B2L2v R+r
则
△t=m△v,B2L2v R+r
v△t=m△v,B2L2 R+r
则
△x=m△v,B2L2 R+r
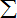
△x=B2L2 R+r
m△v,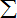
B2L2 R+r
△x=m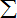
△v,
求和,解得:
x=mv,B2L2 R+r
则x=
=36m;mv(R+r) B2L2
答:(1)棒ab刚进入磁场时的加速度大小为4m/s2;
(2)进入磁场到此时的过程中电阻R产生的焦耳热为36J;
(3)棒ab最终停的位置距MN36m.
