参考题两根相距d=0.20m的平行光滑金属长导轨与水平方向成30°角固定，匀强磁场的磁感强度B=0.20T，方向垂直两导轨组成的平面，两根金属棒ab．cd互相平行且始终与导轨垂直地放在导轨上，它们的质量分别为m1=0.1kg，m2=0.02kg，两棒电阻均为0.20Ω，导轨电阻不计，如图所示．
（1）当ab棒在平行于导轨平面斜向上的外力作用下，以v1=1.5m/s速度沿斜面匀速向上运动，求金属棒cd运动的最大速度；
（2）若要cd棒静止，求使ab匀速运动时外力的功率．（g=10m/s2）
（1）刚释放cd棒时，ab棒产生的感应电动势：E=BLv0=0.2×0.2×1.5V=0.06V
刚释放时cd棒时，由欧姆定律得：I=
=E 2R
A=0.15A0.06 2×0.2
cd所受安培力大小为：F安=BIL=0.2×0.15×0.2N=0.06N，
由左手定则判断可知，安培力方向沿导轨向上．
又cd棒的重力沿斜面向下的分力为：m2gsinθ=0.02×10×sin30°=0.1N
可知F安＜m2gsinθ，所以cd棒将沿导轨向下运动，做匀速直线运动，速度达到最大．
对cd杆有：m2gsinθ=BIL
则：I=
=m2gsinθ BL
=2.5A0.02×10×sin30° 0.2×0.2
感应电流为：I=
，则感应电动势为 E=2IR=2×2.5×0.2V=1VE 2R
总的感应电动势为：E=BLv1+BLv2
由以上各式解得：v2=
-v1=E BL
-1.5=23.5m/s1 0.2×0.2
（2）当cd静止时：感应电动势为：E=BLv1
感应电流为：I=E 2R
对cd杆有：m2gsinθ=BIL
对杆ab有：F-BIL-m1gsinθ=0
解得：F=（m1+m2）gsinθ=（0.1+0.02）×10×sin30°=0.6N
解得：v1=
=2m2gRsinθ B2L2
=25m/s2×0.02×10×0.2×sin30° 0．22×0．22
外力的功率为：P=Fv1=0.6×25W=15W
答：（1）金属棒cd运动的最大速度是23.5m/s；
（2）若要cd棒静止，使ab匀速运动时外力的功率为15W．
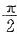的曲率k=______．