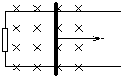
如图,固定于水平地面上接有阻值为R=0.50Ω的电阻的光滑金属框架上放置一金属棒ab,金属框架宽度为L=1.0m,垂直于质量为m=1.0kg的金属棒ab施加一水平恒力F=1.0N,使棒从静止开始运动,当速度达到最大值时,电阻R上产生的焦耳热为Q=0.50J,整个装置处于竖直向下的匀强磁场中,磁感应强度为B=1.0T,金属棒的电阻为r=0.50Ω,不计其它电阻,求:
(1)金属棒的最大速度v;
(2)达到最大速度时金属棒在框架上运动的位移S;
(3)金属棒从静止开始运动到最大速度所需要的时间t.
(1)当金属棒匀速运动时,速度最大.以最大速度运动时产生的感应电动势为:E=BLv
回路中的感应电流为:I=E R+r
达到最大速度时金属棒所受外力与安培力大小相等,即:F=F安=BIL
由以上各式解得金属棒的最大速度为:v=
=F(R+r) B2L2
m/s=1m/s 1×(0.5+0.5) 12×12
(2)根据能量守恒定律得:FS=Q+
mv21 2
得:S=
=Q+
mv21 2 F
=1m0.5+
×1×121 2 1
(3)设金属棒从静止开始运动到最大速度通过金属棒的电量为q.
则根据法拉第电磁感应定律:感应电动势平均值为:
=. E △Φ △t
感应电流的平均值为:
=. I . E R+r
电量 q=
△t. I
联立以上三式得:q=
=△Φ R+r
=BLS R+r
C=1C1×1×1 0.5+0.5
根据动量定理得:Ft-B
L•△t=mv-0. I
即得:Ft-BqL=mv
则得:t=
=mv+BqL F
s=2s1×1+1×1×1 1
答:(1)金属棒的最大速度v是1m/s;
(2)达到最大速度时金属棒在框架上运动的位移S是1m;
(3)金属棒从静止开始运动到最大速度所需要的时间t是2s.