问题
问答题
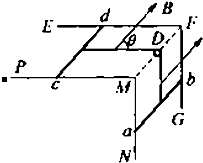
不计电阻的光滑平行轨道EFG、PMN构成相互垂直的L型,磁感应强度为B的匀强磁场方向与水平的EFMP平面夹角θ(θ<45°)斜向上,金属棒ab、cd的质量均为m、长均为L、电阻均为R.ab、cd由细线通过角顶处的光滑定滑轮连接,细线质量不计,ab、cd与轨道正交,已知重力加速度为g.
(1)求金属棒的最大速度vmax;
(2)当金属棒速度为v时,且v小于最大速度vmax时,求机械能损失的功率P1和电阻的发热功率P2.
答案
(1)金属棒达到最大速度vmax时,回路中的感应电动势为:E=BLvmaxcosθ-BLvmaxsinθ
回路中感应电流:I=E 2R
当两棒均做匀速运动时,棒的速度达最大值,故有:
mg=BILcosθ-BILsinθ
联立得:vmax=
.2mgR B2L2(cosθ-sinθ)2
(2)当金属棒速度为v时,且v小于最大速度vmax时,机械能损失的功率P1等于电阻的发热功率P2,且均为:P1=P2=
=E′2 2R B2L2v2(cosθ-sinθ)2 2R
答:(1)金属棒的最大速度vmax为
.2mgR B2L2(cosθ-sinθ)2
(2)当金属棒速度为v时,且v小于最大速度vmax时,机械能损失的功率P1为
,电阻的发热功率P2为B2L2v2(cosθ-sinθ)2 2R
.B2L2v2(cosθ-sinθ)2 2R
