问题
问答题
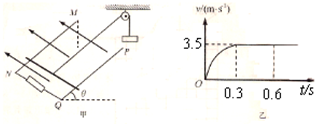
如图甲所示,一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L=1.0m,NQ两端连接阻值R=3.0Ω的电阻,磁感应强度为B的匀强磁场垂直于导轨所在平面向上,导轨平面与水平面间的夹角θ=300.一质量m=0.20kg,阻值r=0.50Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M=0.60kg的重物相连.细线与金属导轨平行.金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示,已知金属棒在0~0.3s内通过的电量是0.3~0.6s内通过电量的
,g=10m/s2,求:1 3
(1)0~0.3s内棒通过的位移;
(2)金属棒在0~0.6s内产生的热量.
答案
(1)金属棒在0.3~0.6s内通过的电量是q1=I1t1=
.BLvt1 R+r
金属棒在0~0.3s内通过的电量q2=
=△Φ R+r
.BLx2 R+r
由题:q1=3q2,
代入解得:x2=0.35m
(2)金属棒在0~0.6s内通过的总位移为x=x1+x2=vt1+x2,代入解得x=1.4m
根据能量守恒定律
Mgx-mgxsinθ-Q=
(m+M)v21 2
代入解得 Q=2.1J
由于金属棒与电阻R串联,电流相等,根据焦耳定律Q=I2Rt,得到它们产生的热量与电阻成正比,所以金属棒在0~0.6s内产生的热量量Qr=
Q=0.3J.r r+R
答:(1)0~0.3s内棒通过的位移为0.35m;
(2)金属棒在0~0.6s内产生的热量为0.3J.
