问题
问答题
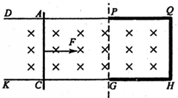
如图所示,相距为L的两条足够长光滑平行金属导轨固定在水平面上,导轨由两种材料组成.PG右侧部分单位长度电阻为r0,且PQ=QH=GH=L.PG左侧导轨与导体棒电阻均不计.整个导轨处于匀强磁场中,磁场方向垂直于导轨平面向下,磁感应强度为B.质量为m的导体棒AC在恒力F作用下从静止开始运动,在到达PG之前导体棒AC已经匀速.
(1)求当导体棒匀速运动时回路中的电流;
(2)若导体棒运动到PQ中点时速度大小为v1,试计算此时导体棒加速度;
(3)若导体棒初始位置与PG相距为d,运动到QH位置时速度大小为v2,试计算整个过程回路中产生的焦耳热.
答案
(1)导体棒匀速运动时拉力与安培力平衡,根据平衡条件得:F=BIL,
得:I=F BL
(2)导体棒运动到PQ中点时速度大小为v1,产生的感应电动势为:E=BLv1
闭合回路中总电阻为:R=2Lr0
感应电流为:I=E R
导体棒AC所受安培力大小为:FA=BIL
联立得:FA=
=B2L2v1 2Lr0 B2Lv1 2r0
根据牛顿第二定律得:F-
=maB2Lv1 2r0
则得:a=
-F m B2Lv1 2mr0
(3)根据能量守恒定律得:Q=F(d+L)-
m1 2 v 22
答:(1)当导体棒匀速运动时回路中的电流为
;F BL
(2)计算此时导体棒加速度为
-F m
;B2Lv1 2mr0
(3)整个过程回路中产生的焦耳热为F(d+L)-
m1 2
.v 22
