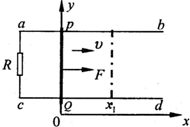
如图所示,固定于水平面的U型金属导轨abcd,电阻不计,导轨间距L=1.0m,左端接有电阻R=2Ω.金属杆PQ的质量m=0.2Kg,电阻r=1Ω,与导轨间动摩擦因数μ=0.2,滑动时保持与导轨垂直.在水平面上建立x0y坐标系,x≥0的空间存在竖直向下的磁场,磁感应强度仅随横坐标x变化.金属杆受水平恒力F=2.4N的作用,从坐标原点开始以初速度v0=1.0m/s向右作匀加速运动,经t1=0.4s到达x1=0.8m处,g取10m/s2.
求:
(1)磁感应强度与横坐标x应满足的关系;
(2)金属杆运动到x1处,PQ两点间的电势差;
(3)金属杆从开始运动到B=
T处的过程中克服安培力所做的功.3 2
(1)设金属杆运动的加速度为a,则
由x1=v0t+
a1 2
得:a=5m/s2t 21
杆运动到坐标x处的速度为v,则:v2-
=2axv 20
杆中产生感应电动势:E=BLv=BL
+2axv 20
杆受到的安培力:FA=BIL=B
L=E R+r B2L2
+2axv 20 R+r
由牛顿第二定律得:F-μmg-FA=ma
即:F-μmg-
=maB2L2
+2axv 20 R+r
代入数据得:B=3 1+10x
(2)金属杆PQ运动到x1处,速度v1,磁感应强度B1
由
-v 21
=2ax1得:B1=1Tv 20
此时杆中的电动势E1=B1Lv1=3V
则PQ两点的电势差:U=
E1=2VR R+r
(3)当金属杆运动到B=
T处,由(1)知对应的坐标为x2=1.5m,3 2
速度v2=
=4m/s
+2ax2v 20
设金属杆PQ从开始运动到B=
T处的过程中克服安培力做的功为WA3 2
根据动能定理:Fx2-μmgx2-WA=
m1 2
-v 22
m1 2 v 20
代入数据得:WA=1.5J
答:(1)磁感应强度与横坐标x应满足的关系为B=
;3 1+10x
(2)金属杆运动到x1处,PQ两点间的电势差为2V;
(3)金属杆从开始运动到B=
T处的过程中克服安培力所做的功为1.5J.3 2
