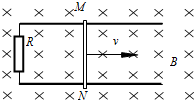
如图所示,宽度为L=0.40m的足够长的平行光滑金属导轨固定在绝缘水平面上,导轨的一端连接阻值为R=2.0Ω的电阻.导轨所在空间存在竖直向下的匀强磁场,磁感应强度大小为B=0.40T.一根质量为m=0.1kg的导体棒MN放在导轨上与导轨接触良好,导轨和导体棒的电阻均可忽略不计.现用一平行于导轨的拉力拉动导体棒沿导轨向右匀速运动,运动速度v=0.50m/s,在运动过程中保持导体棒与导轨垂直.求:
(1)在闭合回路中产生的感应电流的大小;
(2)作用在导体棒上的拉力的大小及拉力的功率;
(3)当导体棒移动50cm时撤去拉力,求整个运动过程中电阻R上产生的热量.
(1)感应电动势:E=BLv=0.40×0.40×0.5V=8.0×10-2V,
感应电流为:I=
=E R
A=4.0×10-2A,8.0×10-2 2.0
(2)导体棒匀速运动,安培力与拉力平衡:
F=FB=BIL=0.40×4.0×10-2×0.4N=6.4×10-3N,
拉力的功率为:P=Fv=6.4×10-3×0.50W=3.2×10-3W;
(3)导体棒移动35cm的时间为:t=
=x v
=1.0s,0.5m 0.5m/s
根据焦耳定律:Q1=I2Rt=0.042×2.0×1.0J=3.2×10-3J,
由能量守恒定律得:Q2=
mv2=1 2
×0.1×0.502J=1.25×10-2J,1 2
电阻R上产生的热量:Q=Q1+Q2=3.2×10-3+1.25×10-2J=1.57×10-2J;
答:(1)在闭合回路中产生的感应电流的大小是4.0×10-2A;
(2)作用在导体棒上的拉力的大小是6.4×10-3N,拉力的功率是3.2×10-3W;
(3)整个运动过程中电阻R上产生的热量为1.57×10-2J.