问题
问答题
如图甲所示,光滑平行导轨MN、PQ固定于同一水平面内,导轨相距L=0.2m,导轨左端接有规格为“0.6V,0.6W”的小灯泡,磁感应强度B=1T的匀强磁场垂直于导轨平面,导体棒ab与导轨垂直并接触良好,在水平拉力作用下沿导轨向右运动,此过程中小灯泡始终正常发光,已知导轨MN、PQ与导体棒的材料相同,每米长度的电阻r=0.5Ω,其余导线电阻不计,导体棒的质量m=0.1kg,导体棒到左端MP的距离为x.
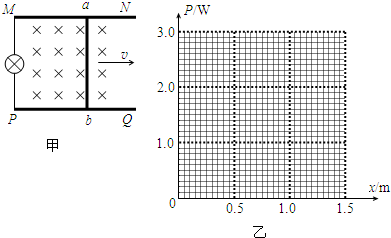
(1)求出导体棒ab的速度v与x的关系式;
(2)在图乙所给坐标中准确画出aMPba回路的电功率P与x的关系图象(不必写出分析过程,只根据所画图象给分);
(3)求出导体棒从x1=0.1m处运动到x2=0.3m处的过程中水平拉力所做的功.
答案
(1)导体棒接入电路的电阻R0=0.2×0.5Ω=0.1Ω
灯泡正常发光,由P=UI得电路中电流I=
=1AP U
灯泡电阻R灯=
=0.6ΩU I
ab切割磁场产生感应电动势E=Blv
根据闭合电路欧姆定律有I=E R0+R灯+2xr
综合上述各式,代入数据后得v=(5x+3.5)m/s
(2)如图所示:

(3)x1=0.1m时,速度v1=4m/s,x2=0.3m时,速度v2=5m/s
根据动能定理可得W拉+W安=
mv22-1 2
mv121 2
其中安培力所做的功W安=-BIL△x
解得W拉=0.49J
答:(1)导体棒ab的速度v与x的关系式为v=(5x+3.5)m/s
(2)电功率P与x的关系图象如图所示:
(3)水平拉力所做的功为0.49J.
