如图所示，间距L=1m的足够长的光滑平行金属导轨与水平面成30°角

问题问答题

如图所示，间距L=1m的足够长的光滑平行金属导轨与水平面成30°角放置，导轨电阻不计，导轨上端连有R=0.8Ω的电阻，磁感应强度为B=1T的匀强磁场垂直导轨平面向上，t=0时刻有一质量m=1kg，电阻r=0.2Ω的金属棒，以v₀=10m/s的初速度从导轨上某一位置PP'开始沿导轨向上滑行，金属棒垂直导轨且与导轨接触良好，与此同时对金属棒施加一个沿斜面向上且垂直于金属棒的外力F，使金属棒做加速度大小为2m/s²的匀减速直线运动，则：

（1）t=2s时，外力F的大小？

（2）若已知金属棒运动从开始运动到最高点的过程中，电阻R上产生的热量为100J，求此过程中外力F做的功？

（3）到最高点后，撤去外力F，经过足够长时间后，最终电阻R上消耗的热功率是多少？

答案

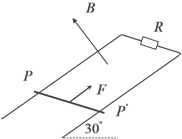
（1）金属棒匀加速上升，根据速度时间关系公式，有：

v₁=v₀+at=10-2×2=6m/s

对金属棒受力分析，受重力、支持力、安培力，如图所示：

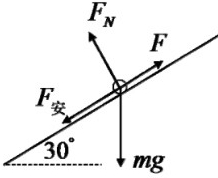
根据平衡条件，有：

mgsin30°+F_安-F=ma

其中：

F_安=BI₁L

I₁=

R+r

E₁=BLv₁

解得：F=9N

（2）根据速度位移关系公式，到最高点的位移：

=25m

由动能定理，得：

W_F-mgxsin30°-Q_总=0-

其中：Q_总=

R+r

QR=125J

解得：W_F=200J

（3）如图所示，最后稳定时导体棒的速度满足：

mgsin30°=

B2L2v

R+r

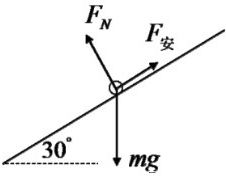
电功率等于克服安培力做功的功率，故：

P_电=P_安=mgvsin30°=25W

根据功率分配关系，有：

P_R=

R+r

P电=20W

答：（1）t=2s时，外力F的大小为9N；（2）此过程中外力F做的功为200J；（3）电阻R上消耗的热功率是20W．