问题
问答题
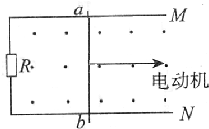
如图所示,水平旋转的平行金属导轨M、N间接一阻值R=0.128Ω的电阻,轨道宽为L=0.8m.轨道上搭一金属棒ab,其质量m=0.4kg,ab与导轨间的动摩擦因数μ=0.5,除R外其余电阻不计,垂直于轨道的匀强磁场的磁感应强度为B=2T,ab在一电动机的牵引下由静止开始运动,经过t=2s,ab运动了s=1.2m,刚好达到最大速度.此过程中电动机的平均输出功率为8W,最大输出功率14.4W.求:
(1)金属棒ab运动的最大速度多大?
(2)该过程中电阻R上消耗的电能.(g=10m/s2)
答案
(1)速度最大时,加速度为零,
则有F-μmg-BIL=0①
设最大速度为vm,
则有:F=
②Pm vm
电流I=
③BLvm R
把②③代入①得:B2L2 R
+μmgvm-Pm=0,v 2m
解得:Vm=0.8m/s
(2)根据动能定理:
×t-μmg×s-WA=. P
m1 2
-0v 2m
克服安培力做的功全部转化为电能,电能消耗在电阻R上,
则有:WR=W安
根据动能定理知:
t-μmg-W安=. P
m1 2
-0v 2m
代入数据解得WR=13.472J
答:(1)金属棒ab运动的最大速度为0.8m/s;
(2)该过程中电阻R上消耗的电能13.472J.
