如图甲所示,空间存在一宽度为2L有界匀强磁场,磁场方向垂直纸面向里.在光滑绝缘水平面内有一边长为L的正方形金属线框,其质量m=1kg、电阻R=4Ω,在水平向左的外力F作用下,以初速度v0=4m/s匀减速进入磁场,线框平面与磁场垂直,外力F大小随时间t变化的图线如图乙所示.以线框右边刚进入磁场时开始计时,求:
(1)匀强磁场的磁感应强度B;
(2)线框进入磁场的过程中,通过线框的电荷量q;
(3)判断线框能否从右侧离开磁场?说明理由.
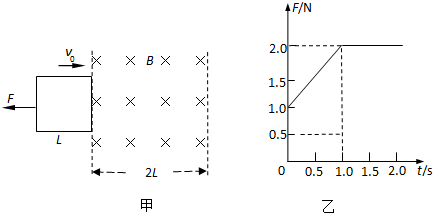
(1)由F-t图象可知,线框加速度a=
=2m/s2F2 m
线框的边长L=v0t-
at2=(4×1-1 2
×2×12)m=3m1 2
t=0时刻线框中的感应电流I=BLv0 R
线框所受的安培力F安=BIl
由牛顿第二定律F1+F安=ma
又F1=1N
联立得:B=
T=0.33T1 3
答:匀强磁场的磁感应强度:B=
T=0.33T.1 3
(2)线框进入磁场的过程中,平均感应电动势
=. E BL2 t
平均电流
=. I . E R
通过线框的电荷量q=
t. I
联立得:q=0.75C
答:线框进入磁场的过程中,通过线框的电荷量q=0.75C.
(3)设匀减速运动速度减为零的过程中线框通过的位移为x,
由运动学公式得0-v02=-2ax
代入数值得x=4m<2L
所以线框不能从右侧离开磁场.
