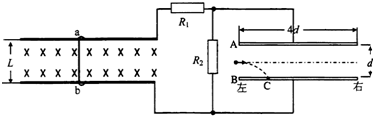
如图,足够长平行金属导轨内有垂直纸面向里的匀强磁场,金属杆ab与导轨垂直且接触良好,导轨右端通过电阻与平行金属板AB连接.已知导轨相距为L;磁场磁感应强度为B;R1、R2和ab杆的电阻值均为r,其余电阻不计;板间距为d、板长为4d;重力加速度为g,不计空气阻力.
如果ab杆以某一速度向左匀速运动时,沿两板中心线水平射入质量为m、带电量为+q的微粒恰能沿两板中心线射出;如果ab杆以同样大小的速度向右匀速运动时,该微粒将射到B板距左端为d的C处.
(1)求ab杆匀速运动的速度大小v;
(2)求微粒水平射入两板时的速度大小v0;
(3)如果以v0沿中心线射入的上述微粒能够从两板间射出,试讨论ab杆向左匀速运动的速度范围.
(1)带电量为+q的微粒恰能沿两板中心线射出,此时电场力与重力平衡,设场强为E,则:
mg=Eq①
此时平行板间电压为;
U=Ed②
导体棒感应电动势为:E感=BLv
由电路欧姆定律得:U=
E感③1 3
联立以上可得:v=
④3mgd BLq
(2)ab杆以同样大小的速度向右匀速运动时,平行板间带电粒子所受合力方向向下,大小为;
F=Eq+mg=2mg⑤
粒子做类平抛运动,可知加速度为:
a=2g⑥
打到板的时间为t,则:
=d 2
at2⑦1 2
d=v0t⑧
联立解得:v0=
⑨2gd
(3)ab杆向左匀速运动时,电场力与重力方向相反,棒速度较小则向下偏,较大则向上偏,粒子做类平抛运动,若粒子恰好射出电场,在水平位移应为L=4d时间内,同时竖直位移恰为
,d 2
故粒子运动时间:
4d=v0t1⑩
若向下偏,最小加速度大小为a1,则竖直方向位移为:
a11 2
=t 21
(11)d 2
⑦⑧⑩(11)得:a1=
=a 4
(12)g 8
设此时导体棒速度最小为vmin,应有:
a1=
=g-mg-
qBLvmin 3 d m
(13)BLvminq 3md
解得vmin=
,21mg 32Bq
若导体棒速度最大为vmax,此时粒子向上偏转,应有:
a1=
=a ′1
=
q-mgBLvmax 3 d m
-gBLvmaxq 3dm
解得:vmax=27mg 32Bq
ab杆向左匀速运动的速度范围为
<v<21mg 32Bq 27mg 32Bq
答:(1)ab杆匀速运动的速度为3mgd BLq
(2)微粒水平射入两板时的速度2gd
(3)ab杆向左匀速运动的速度范围为
<v<21mg 32Bq 27mg 32Bq