问题
问答题
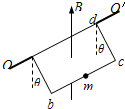
如图所示,将一根质量为M=0.06kg的均匀导线杆弯成矩形闭合导线框abcd,其ab=cd=L1=0.1m,bc=ad=L2=0.2m.它的ad边由aO、dO′两轴承支撑沿水平放置,导线框位于竖直平面内,bc段中点固定一质量为m=0.02kg的小金属球,整个装置处在一方向竖直向上的匀强磁场中.当导线框中通以大小恒为1A的恒定电流I时,整个装置以OO′为轴从静止开始逆时针转动.
(1)在图中画出导线框bc段中的电流方向;
(2)若导线框运动过程中与竖直方向的最大偏角θ为37°,则匀强磁场的磁感应强度B1为多大?(已知sin37°=0.6,cos37°=0.8)
(3)若已知磁感应强度B2=1T,则导线框在运动过程中,速度达到最大时,与竖直方向的偏角α为多大.
答案
(1)根据受力平衡,从而确定安培力的方向,再由左手定则,可确定电流方向为:b→c;
(2)根据动能定理可知,B1IL2L1sinθ-mgL1(1-cosθ)-Mg(1-cosθ)=△Ek,
解得B1=
T;5 6
(3)速度最大时,整个装置处于力矩平衡状态,
则有:B2IL2L1cosα=mgL1sinα+Mgsinα,
得α=arctan0.4.
答:(1)在图中画出导线框bc段中的电流方向:b→c;
(2)若导线框运动过程中与竖直方向的最大偏角θ为37°,则匀强磁场的磁感应强度B1为=
T;5 6
(3)若已知磁感应强度B2=1T,则导线框在运动过程中,速度达到最大时,与竖直方向的偏角α为arctan0.4.
