问题
解答题
已知向量p=（a+c，b），q=（a-c，b-a）且p·q=0，其中角A、B、C是△ABC的内角，a、b、c分别是角A、B、C的对边。
（1）求角C的大小；
（2）求sinA+cosB的取值范围。
答案
解：（1）由p·q=0，得（a+c）（a-c）+b（b-a）=0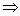
a2+b2-c2=ab
由余弦定理得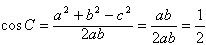
∵
∴
；
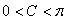
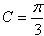（2）∵
∴
∴
∴
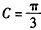
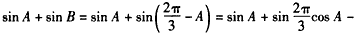
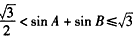
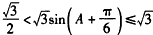
即。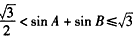
搜题请搜索小程序“爱下问搜题”
已知向量p=（a+c，b），q=（a-c，b-a）且p·q=0，其中角A、B、C是△ABC的内角，a、b、c分别是角A、B、C的对边。
（1）求角C的大小；
（2）求sinA+cosB的取值范围。
解：（1）由p·q=0，得（a+c）（a-c）+b（b-a）=0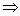a2+b2-c2=ab
由余弦定理得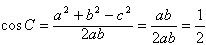
∵
∴；
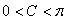
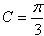（2）∵
∴
∴
∴
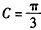
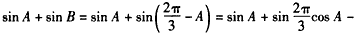
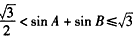
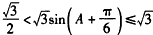
即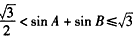。