问题
单项选择题
设A，Dj（j=1，2，…，n）分别为线性方程组AX=b的n阶系数矩阵和系数矩阵第了列元素换成常数项后对应的行列式，则（）。
A．若|A|＝o，则线性方程组有无穷多解
B．若|A|＝0，且Dj＝0(j＝1，2，…，72)，则线性方程组有无穷多解
C．若|A|＝0，则线性方程组无解
D．若|A|≠0，则线性方程组有唯一解
答案
参考答案：D
解析：
根据克莱姆法则，当其系数行列式，|A|≠0时，线性方程组AX＝b有唯一解，选D。其余选项中都有，|A|＝0，R(A) ＜n，解的情况须比较系数矩阵秩及(A) 与增广矩阵秩R(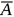
)，R(A) ＝R(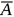)＜n，有无穷多解，R(A) ＜R(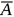)时无解，A、 B、C三种选项都不能肯定成立。 [点评] 本题考察线性方程组AX＝b的克莱姆法则、系数矩阵秩和线性方程组有唯一解、无穷多解、无解的关系。