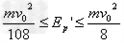问题
计算题
如图所示,在光滑水平长直轨道上,A、B两小球之间有一处于原长的轻质弹簧,弹簧右端与B球连接,左端与A球接触但不粘连,已知 ,开始时A、B均静止。在A球的左边有一质量为
,开始时A、B均静止。在A球的左边有一质量为 的小球C以初速度v0,与A球碰撞后粘连在一起,成为一个复合球D,碰撞时间极短。接着逐渐压缩弹簧并使B球运动.经过一段时间后,D球与弹簧分离(弹簧始终处于弹性限度内)。
的小球C以初速度v0,与A球碰撞后粘连在一起,成为一个复合球D,碰撞时间极短。接着逐渐压缩弹簧并使B球运动.经过一段时间后,D球与弹簧分离(弹簧始终处于弹性限度内)。
(1)上述过程中,弹簧的最大弹性势能是多少?
(2)当弹簧恢复原长时B球速度是多大?
(3)若开始时在B球右侧某位置固定一块挡板(图中未画出),在D球与弹簧分离前使B球与挡板发生碰撞,并在碰后立即将挡板撤走,设B球与挡板碰撞时间极短,碰后B球速度大小不变,但方向相反。试求出此后弹簧的弹性势能最大值的范围。

答案
解:(1)C与A相碰后速度为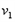 ,三个球共同速度为
,三个球共同速度为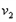
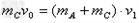 ,得
,得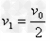
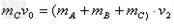 ,得
,得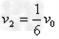
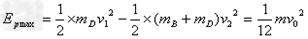
(2)设弹簧恢复原长时,D球速度为 ,B球速度为
,B球速度为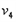
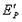
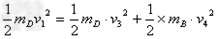
得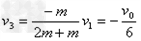 ,
,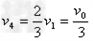
(3)设B球与档板相碰前瞬间D、B两球速度为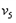 、
、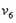
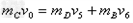
与档板碰后弹性势能最大(设为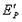 ),则D、B两球速度相等,设为
),则D、B两球速度相等,设为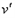
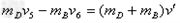
整理得
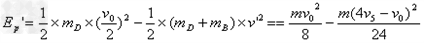
当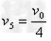 时,
时,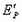 最大,
最大,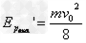
当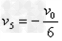 时,
时,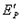 最小,
最小,