问题
解答题
求由曲线y=x2+2，x+y=4所围成的封闭图形的面积．
答案
如图，
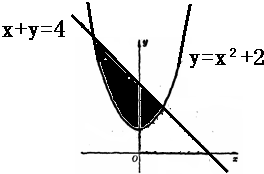
由曲线y=x2+2，x+y=4所围成的封闭图形的面积
S=
[(4-x)-(x2+2)]dx=∫ 1-2
(2-x-x2)dx=(2x-∫ 1-2
x2-1 2
x3)1 3
=| 1-2
…（8分）9 2
搜题请搜索小程序“爱下问搜题”
求由曲线y=x2+2，x+y=4所围成的封闭图形的面积．
如图，
由曲线y=x2+2，x+y=4所围成的封闭图形的面积
S=
[(4-x)-(x2+2)]dx=∫ 1-2
(2-x-x2)dx=(2x-∫ 1-2
x2-1 2
x3)1 3
=| 1-2
…（8分）9 2