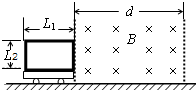
如图所示,水平面上有一个动力小车,在动力小车上竖直固定着一个长度L1、宽度L2的矩形线圈,线圈匝线为n,总电阻为R,小车和线圈的总质量为m,小车运动过程所受摩擦力为f.小车最初静止,线圈的右边刚好与宽为d(d>L1)的有界磁场的左边界重合.磁场方向与线圈平面垂直,磁感应强度为B.现控制动力小车牵引力的功率,让它以恒定加速度a进入磁场,线圈全部进入磁场后,开始做匀速直线运动,直至完全离开磁场,整个过程中,牵引力的总功为W.
(1)求线圈进入磁场过程中,感应电流的最大值和通过导线横截面的电量.
(2)求线圈进入磁场过程中,线圈中产生的焦耳热.
(3)写出整个过程中,牵引力的功率随时间变化的关系式.
(1)全部进入磁场时速度:v=
最大电动势:Em=nBL2v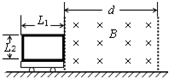
最大电流为:Im==
q=△t=•△t=n•=n=
(2)设进入和离开磁场过程中,线圈产生的焦耳热分别为Q入和Q出,则在整个过程中,
牵引力的总功:W=Q入+Q出+f(L1+d)+mv2
Q出=Rt出,
t出=;
将Im及v代入
得:Q出=
解得:Q入=W-f(L1+d)-maL1-
(3)①小车进入磁场阶段做匀加速运动:
0<t<,vt=at,I=
由-f-nBIL2=ma得:P=t2+(f+ma)at,(0<t<)
②小车完全在磁场中运动:P=f,(<t<(+))
③小车匀速穿出磁场的过程:P=(F安+f)v
得P=+f((+)<t<(+))
答:
(1)线圈进入磁场过程中,感应电流的最大值是,通过导线横截面的电量.
(2)线圈进入磁场过程中,线圈中产生的焦耳热是W-f(L1+d)-maL1-.
(3)在整个过程中,牵引力的功率随时间变化的关系式是)①小车进入磁场阶段做匀加速运动:
P=t2+(f+ma)at,(0<t<)
②小车完全在磁场中运动:P=f,(<t<(+))
③小车匀速穿出磁场的过程:P=+f((+)<t<(+)).


