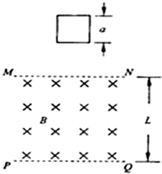
如图所示,水平方向大小为B的匀强磁场的上下边界分别是MN、PQ,磁场宽度为L,一个边长为a的正方形导线框(L>2a)从磁场上方竖直下落,线框的质量为m,电阻为R,运动过程中上下两边始终与磁场边界平行,若线框进入磁场过程中感应电流保持不变.(运动过程中空气阻力不计,重力加速度为g.)求:(1)线框下端进入磁场时的速度.
(2)线框下端即将离开磁场时线框的加速度.
(3)若线框上端离开磁场时线框恰好保持平衡,求线框离开磁场的过程中流经线框电量q和线框完全通过磁场产生的热量Q.
(1)线框进入磁场时电流保持不变,I=Bav R
线框匀速进入磁场,受力平衡,则有:mg=BIa
联立求解可得:v=mgR B2a2
(2)线框完全进入磁场后做匀加速运动,设线框下端即将离开磁场时速度为V′,则
v′2-v2=2g(L-a)
此时线框受到的安培力为 F=Ba
=Bav′ R
、重力mg,则加速度为 a=B2a2v′ R F-mg m
联立解得:a=B2a2 mR
-g,方向竖直向上.
+2g(L-a)m2g2R2 B4a4
(3)当线框上端离开磁场时恰好保持平衡,说明线框受到的安培力与重力相等.
则线框上端离开磁场时与线框下端进入磁场时速度相等均为v,离开磁场时线框做加速度逐渐减小的减速运动,设这段过程中平均电流为
,. I
流过线框的电流q=
△t=. I
△t=. E R
=△Φ R Ba2 R
线框通过磁场全过程产生的热量等于安培力做功的负值:Q=-W安
取线框下端进入磁场到线框上端离开磁场为研究过程,根据能量守恒定律得:
Q=mg(L+a)
答:(1)线框下端进入磁场时的速度为
.mgR B2a2
(2)线框下端即将离开磁场时线框的加速度为B2a2 mR
-g,方向竖直向上.
+2g(L-a)m2g2R2 B4a4
(3)若线框上端离开磁场时线框恰好保持平衡,线框离开磁场的过程中流经线框电量q是
,线框完全通过磁场产生的热量Q为mg(L+a).Ba2 R
