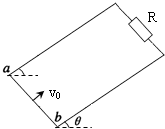
如图所示,质量为m,阻值为R的导体棒ab垂直放在光滑足够长的U形导轨的底端,U形导轨的顶端连接一个阻值为R的电阻,导轨平面与水平面成θ角,整个装置处在与导轨平面垂直的匀强磁场中.现给导体棒沿导轨向上的初速度v0,在导体棒上升到最高点的过程中电阻上产生了Q的热量,返回过程中,导体棒在到达底端前已经做匀速运动,速度大小为
.导轨电阻不计,重力加速度为g.求:v0 4
(1)导体棒从开始运动到返回底端的过程中,回路中产生的电热;
(2)导体棒上升的最大高度.
(3)导体棒在底端开始运动时的加速度大小.
(1)根据能量守恒定律,得:
Q总=
mv02-1 2
m(1 2
)2=v0 4
…①15mv02 32
(2)设上升的最大高度为h,由动能定理有:
-mgh+WF安=0-
mv02…②1 2
电阻R上产生的热量为Q,导体棒与电阻的阻值相等,则整个回路上升过程中产生的热量为2Q,
WF安=-2Q…③
h=
…④mv02-4Q 2mg
(3)在底端,设棒上电流为I,加速度为a,由牛顿第二定律,则:mgsinθ+BIL=ma…⑤
由欧姆定律,得:I=
…⑥E 2R
E=BLv0…⑦
棒到达底端前已经做匀速运动mgsinθ=
…⑧B2L2 v0 4 2R
以上方程联立可得:a=5gsinθ…⑨
答:(1)回路中产生的电热1 5mv 20 32
(2)导体棒上升的最大高度
-4Qmv 20 2mg
(3)导体棒在底端开始运动时的加速度大小5gsinθ.
