问题
问答题
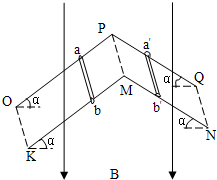
如图所示，两根完全相同的“V”字形导轨OPQ与KMN倒放在绝缘水平面上，两导轨都在竖直平面内且正对、平行放置，其间距为L，电阻不计．两条导轨足够长，所形成的两个斜面与水平面的夹角都是α．两个金属棒ab和a′b′的质量都是m，电阻都是R，与导轨垂直放置且接触良好．空间有竖直向下的匀强磁场，磁感应强度为B．
（1）如果两条导轨皆光滑，让a′b′固定不动，将ab释放，则ab达到的最大速度是多少？
（2）如果将ab与a′b′同时释放，它们所能达到的最大速度分别是多少？
答案
（1）ab运动后切割磁感线，产生感应电流，而后受到安培力，当受力平衡时，加速度为0，速度达到最大，受力情况如图所示．则：
mgsinα=F安cosα
又F安=BIL，E感=BLvmcosα，I=BLvmcosα 2R
联立上式解得：vm=
．2mgRsinα B2L2cos2α
（2）若将ab、a′b′同时释放，因两边情况相同，所以达到的最大速度大小相等，设为vm′．这时ab、a′b′都产生感应电动势而且是串联．
∴mgsinα=F安′cosα
又F安′=BI′L，E感′=BLvm′cosα，I′=
=2BLvm′cosα 2R BLvm′cosα R
∴vm′=mgRsinα B2L2cos2α
答：（1）如果两条导轨皆光滑，让a′b′固定不动，将ab释放，则ab达到的最大速度是
．2mgRsinα B2L2cos2α
（2）如果将ab与a′b′同时释放，它们所能达到的最大速度分别是
．mgRsinα B2L2cos2α
图象如图乙所示，则电压表的内阻________，电源电动势是________。 