问题
解答题
求由抛物线y=-x2+4x-3及其在点 M（0，-3）和点N（3，0）处两条切线所围成的图形的面积S。
答案
解：由y=-x2+4x-3，得y′=-2x+4，
所以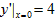
，
所以过M点的切线方程为y=4x-3；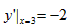
，
所以过N 点的切线方程为y=-2x+6，
所以可求得两切线交点的横坐标为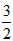
，
故所求面积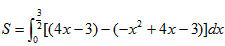
。
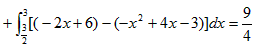搜题请搜索小程序“爱下问搜题”
求由抛物线y=-x2+4x-3及其在点 M（0，-3）和点N（3，0）处两条切线所围成的图形的面积S。
解：由y=-x2+4x-3，得y′=-2x+4，
所以，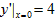
所以过M点的切线方程为y=4x-3；，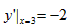
所以过N 点的切线方程为y=-2x+6，
所以可求得两切线交点的横坐标为，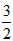
故所求面积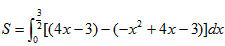。
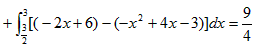