4.8 m/s≥v≥3.8 m/s

A车和人在水平面上向右运动的速度设为v，根据机械能守恒定律

（M₁+M）gh=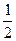(M₁+M)v²，得v=="3" m/s.

情况一：设人以相对地面速度v′跳离A车后，A车以速度v₁向右运动，此过程动量守恒，方程为(M₁+M)v=M₁v₁+Mv′                                                       ①

人跳到B车上，设共同速度为v₂

则Mv′-M₂v₀=(M+M₂)v₂                                                        ②

将已知量代入①②两式，可得210=20v₁+50v′                                     ③

50v′-90=100v₂                                                                ④

由③④两式可知50v′=210-20v₁=90+100v₂

显然，只有当v₂≥v₁时，A、B两车才不会相撞.

设v₁=v₂，根据上式即可求得v₁=v₂="1" m/s，v′≥3.8 m/s.

情况二：设人以相对于地面的速度v″跳离A车后，A车以速度v₁′向左运动；人跳上B车后共同速度为v₂′；根据动量守恒定律，可得方程组（M₁+M）v=Mv″-M₁v₁′            ⑤

Mv″-M₂v₀=(M+M₂)v₂′                                                         ⑥

将已知量代入⑤⑥式，可得50v″=210+20v₁′=90+100v₂′

只有v₂′≥v₁′时，A、B两车才不会相撞，因为v₁′过大会导致M₁反向滑上斜坡后，再滑下时v₁′的大小大于v₂′，此时仍会相撞.

设v₁′=v₂′由上式得v₁′=v₂′="1.5" m/s，v″≤4.8 m/s

综合得，要A、B车不发生相撞，人跳离A车时相对地面的速度v应满足4.8 m/s≥v≥3.8 m/s.