问题
解答题
已知向量a=(x-1,-1),b=(x-m,y),(m∈R),且a·b=0。
(Ⅰ)将y表示为x的函数y=f(x);
(Ⅱ)若tanA、tanB是方程f(x)+4=0的两个实根,A、B是锐角△ABC的两个内角,求证:m≥5;
(Ⅲ)对任意实数α ,恒有f(2+cosα)≤0,求证:m≥3。
答案
(Ⅰ)解:∵ ,
,
又∵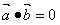 ,
,
∴ ,
,
∴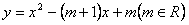 。
。
(Ⅱ)证明:由(Ⅰ)知 ,
,
则方程 ,即为
,即为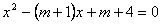 ,
,
依题意,得
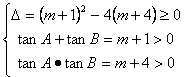 ,
,
又∵A,B为锐角三角形的两内角,
故 ,
,
∴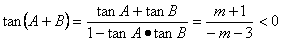 。
。
即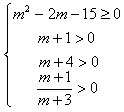 ,
,
解得: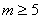 。
。
(Ⅲ)证明:∵
对任意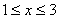 有
有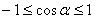 ,
,
即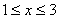 ,恒有
,恒有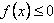 ,即
,即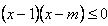 ,
,
∴ ,但
,但 ,
,
∴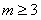 。
。
