问题
问答题
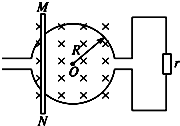
如图所示,半径为R的圆形导轨处在垂直于圆平面的匀强磁场中,磁感应强度为B,方向垂直于纸面向内.一根长度略大于导轨直径的导体棒MN以速率v在圆导轨上从左端滑到右端,电路中的定值电阻为r,其余电阻不计,导体棒与圆形导轨接触良好.求:
(1)在滑动过程中通过电阻r的电流的平均值;
(2)MN从左端到右端的整个过程中,通过r的电荷量;
(3)当MN通过圆导轨中心时,通过r的电流是多大?
答案
(1)由法拉第电磁感应定律可得:E=n
,△? △t
则有:E=B△S △t
而圆形面积为:△S=πR2
导体棒运动的时间为:△t=2R v
再由闭合电路欧姆定律可得:I=
=E r πBRv 2r
(2)MN从左端到右端的整个过程中,通过r的电荷量:q=It
而闭合电路欧姆定律可得:I=E r
由法拉第电磁感应定律可得:E=n△? △t
所以q=
=△? r πBR2 r
(3)当导体棒MN通过圆导轨中心时,
产生的感应电动势为E=BRv
由闭合电路欧姆定律可得::I=E r
所以通过r的电流:I=BRv r
答:(1)在滑动过程中通过电阻r的电流的平均值
;πBRv 2r
(2)MN从左端到右端的整个过程中,通过r的电荷量
;πBR2 r
(3)当MN通过圆导轨中心时,通过r的电流是
.BRv r
