问题
计算题
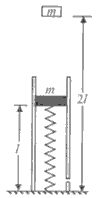
如图所示,有一个竖直固定在地面的透气圆筒,筒中有一轻弹簧,其下端固定,上端连接一质量为m的薄滑块,当滑块运动时,圆筒内壁对滑块有阻力的作用,阻力的大小恒为 (g为重力加速度)。在初始位置滑块静止,圆筒内壁对滑块的阻力为零,弹簧的长度为l。现有一质量也为m的物体从距地面2l处自由落下,与滑块发生碰撞,碰撞时间极短。碰撞后物体与滑块粘在一起向下运动,运动到最低点后又被弹回向上运动,滑动到初始位置时速度恰好为零,不计空气阻力。求:
(g为重力加速度)。在初始位置滑块静止,圆筒内壁对滑块的阻力为零,弹簧的长度为l。现有一质量也为m的物体从距地面2l处自由落下,与滑块发生碰撞,碰撞时间极短。碰撞后物体与滑块粘在一起向下运动,运动到最低点后又被弹回向上运动,滑动到初始位置时速度恰好为零,不计空气阻力。求:
(1)物体与滑块碰撞过程中,合力对物体的冲量的大小;
(2)碰撞后,在滑块向下运动到最低点的过程中弹簧弹力所做的功。
答案
解:(1)设碰撞前物体的速度为v0,有:
设碰撞后共同速度为v,有: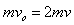
对物体应用动量定理得:
(2)设下滑的最大距离s,由碰撞后开始弹回初始位置的过程中有: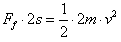
由碰撞后开始运动到最低点的过程中,根据动能定理有: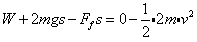
解得: