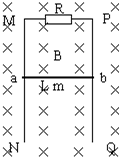
如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,一个磁感应强度为B=0.5T的匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.3Ω的电阻,长为L=0.40m,电阻为r=0.2Ω的金属棒ab紧贴在导轨上.现使金属棒ab由静止开始下滑,通过传感器记录金属棒ab下滑的距离,其下滑的距离与时间的关系如下表所示,导轨的电阻不计.(g=10m/s2)
| 时间t(s) | 0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 |
| 下滑距离s(m) | 0 | 0.10 | 0.30 | 0.70 | 1.20 | 1.70 | 2.20 | 2.70 |
(1)在前0.4s的时间内,金属棒ab电动势的平均值.
(2)在0.7s时,金属棒ab两端的电压值.
(3)在前0.7s的时间内,电阻R上产生的热量Q.
(1)根据法拉第电磁感应定律得:
金属棒ab电动势的平均值
=. E
=△∅ △t
=0.6V.BLs △t
(2)从表格中数据可知,0.3s后棒做匀速运动
速度v=
=5m/s.△s △t
由mg-F=0,F=BIL,
I=
,E=BLv.E R+r
解得m=0.04 Kg
∴ab棒两端的电压,u=E-Ir=0.6V
(3)棒在下滑过程中,有重力和安培力做功,根据动能定理得:
mgs+W安=
mv2-01 2
克服安培力做的功等于回路的焦耳热,
W安=-Q
QR=
QR R+r
解得 Q=0.348J
答:(1)在前0.4s的时间内,金属棒ab电动势的平均值是0.6V.
(2)在0.7s时,金属棒ab两端的电压值是0.6V.
(3)在前0.7s的时间内,电阻R上产生的热量Q是0.348J.
