问题
计算题
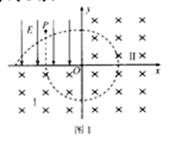
(20分)如图所示,在坐标系xoy的第二象限内有沿y轴负方向的匀强电场,电场强度大小为E第三象限内存在匀强磁场I,y轴右侧区域内存在匀强磁场Ⅱ,I、Ⅱ磁场的方向均垂直于纸面向里。一质量为m、电荷量为+q的粒子自P(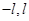 )点由静止释放,沿垂直于x轴的方向进入磁场I,接着以垂直于y轴的方向进入磁场Ⅱ,不计粒子重力.
)点由静止释放,沿垂直于x轴的方向进入磁场I,接着以垂直于y轴的方向进入磁场Ⅱ,不计粒子重力.
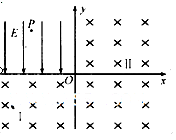
(l)求磁场I的磁感应强度B1;
(2)若磁场Ⅱ的磁感应强度B2=B1,粒子从磁场Ⅱ再次进入电场,求粒子第二次离开电场时的横坐标;
(3)若磁场Ⅱ的磁感应强度B2=3B1,求粒子在第一次经过y轴到第六次经过y轴的时间内,粒子的平均速度.
答案
(1) B1=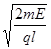 ;(2) x′=-2l;(3)
;(2) x′=-2l;(3)  ,方向沿y轴负方向。
,方向沿y轴负方向。
题目分析:(1)设粒子垂直于x轴进入I时的速度为v,由运动学公式:2al=v2
由牛顿第二定律:Eq=ma
由题意知,粒子在I中做圆周运动的半径为l
由牛顿第二定律qvB1=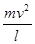 ,得B1=
,得B1=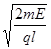 。
。
(2)粒子运动的轨迹如图所示,粒子第二次进入电场,在电场中做类平抛运动
x负方向:x=vt
y负方向:l=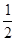 at2
at2
得x=2l,则横坐标x′=-2l。
(3)粒子的运动轨迹如图2所示,
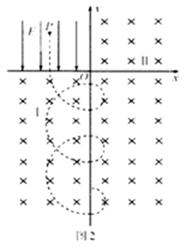
设粒子在磁场I中运动的半径为R1,周期为T1,
在磁场Ⅱ中运动的半径为R2,周期为T2,则R1=l,3qvB= ,
,
则T1=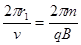 ,T2=
,T2=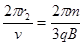 , 得:R2=
, 得:R2=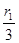 ,T2=
,T2=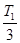 ,
,
粒子在第一次经过 y轴到第六次经过y轴的时间t=T1+ T2
T2
粒子在第一次经过 y轴到第六次经过y轴时间内的位移s=6R2;
平均速度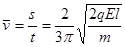 ,方向沿y轴负方向。
,方向沿y轴负方向。
