问题
问答题
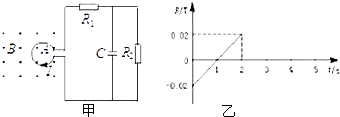
如图甲所示,截面积为0.2m2的100匝圆形线圈A处在变化磁场中,磁场方向垂直线圈截面,其磁感应强度B随时间t的变化规律如图乙所示.设向外为B的正方向,线圈A上的箭头为感应电流I的正方向,R1=4Ω,R2=6Ω,C=30μF,线圈内阻不计.求电容器充电时的电压和2s后电容器放电的电量.其中通过R2的电量是多少?
答案
磁感应强度的变化率为:
=△B △t
T/s=0.02T/s,0.02 1
感应电动势为:E=n
t=nS△∅ △t
=100×0.2×0.02V=0.4V△B △t
通过R2的电流强度为:I=
=E R1+R2
A=0.04A,0.4 4+6
所以:UC=IR2=0.04×6V=0.24V,
2s后磁场消失(B=0),电容器通过电阻和线圈放电;
放电的电量即为充电后电容器上的带电量,
所以:Q=CUC=30×10-6×0.24C=7.2×10-6C.
其中通过R2的电量是总电量的
,QR2=1.44×10-6C.2 5
答:电容器充电时的电压0.24V,和2s后电容器放电的电量7.2×10-6C,其中通过R2的电量是1.44×10-6C.
