问题
多选题
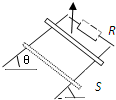
如图相距为L的两光滑平行导轨,平行放置在倾角为θ的斜面上,导轨的右端接有电阻R(轨道电阻不计),斜面处在一匀强磁场B中,磁场方向垂直于斜面向上,质量为m,电阻为2R的金属棒ab放在导轨上,与导轨接触良好,由静止释放,下滑距离S后速度最大,则( )
A.下滑过程电阻R消耗的最大功率为
Rm2g2Sin2θ B2L2
B.下滑过程电阻R消耗的最大功率为
R3m2g2Sin2θ B2L2
C.下滑过程安培力做功
R29m3g2Sin2θ 2B4L4
D.下滑过程安培力做功mgS•sinθ-9m3g2Sin2θ 2B4L4R2
答案
A、对棒受力分析,如图所示,
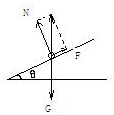
当棒达到最大速度时,处于受力平衡状态,则有:F=mgsinθ;
又F=BIL;
闭合电路欧姆定律有:I=
;E 3R
切割感应电动势为:E=BLvm;
因此联立可得:
=mgsinθB2L2vm 3R
则:vm=
;3mgRsinθ B2L2
所以下滑的最大电功率为:P=Fvm=
R;故A错误,B正确;3m2g2Sin2θ B2L2
C、导体棒下滑过程中,根据动能定理得:
则有:WG-W安=
mv2-0,1 2
解得:安培力做功mgS•Sinθ-
R2.故C错误,D正确;9m3g2Sin2θ 2B4L4
故选:BD.
