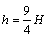如图所示,A、B两个矩形木块用轻弹簧相接静止在水平地面上,弹簧的劲度系数为k,木块A和木块B的质量均为m。
(1)若用力将木块A缓慢地竖直向上提起,木块A向上提起多大高度时,木块B将离开水平地面。
(2)若弹簧的劲度系数k是未知的,将一物体C从A的正上方某位置处无初速释放,C与A相碰后立即粘在一起(不再分离)向下运动,它们到达最低点后又向上运动。已知C的质量为m时,把它从距A高为H处释放,则最终能使B刚好离开地面。若C的质量为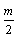 ,要使B始终不离开地面,则释放时,C距A的高度h不能超过多少?
,要使B始终不离开地面,则释放时,C距A的高度h不能超过多少?
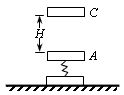
解:(1)开始时,木块A处于平衡,则kx1=mg(弹簧压缩)
木块B刚好离开地面时,有kx2=mg(弹簧伸长)
故木块A向上提起的高度为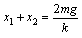
(2)物块C的质量为m时,它自由下落H高度时的速度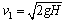 ①
①
设C与A碰撞后的共同速度为v2,根据动量守恒定律,有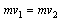
则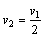 ②
②
以后A、C继续压缩弹簧,后又向上弹起,最终能使木块B刚好离开地面。此过程中,A、C上升的高度为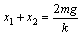 ,由于最初弹簧的压缩量x1与最后的伸长量x2相等,所以,弹簧势能相等,根据机械能守恒定律,有
,由于最初弹簧的压缩量x1与最后的伸长量x2相等,所以,弹簧势能相等,根据机械能守恒定律,有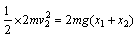 ③
③
物块C的质量为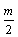 时,设在距A高h处自由下落后刚好能使木块B离开地面
时,设在距A高h处自由下落后刚好能使木块B离开地面
则C下落h高度时的速度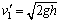 ④
④
设C与A碰撞后的共同速度为 ,则有
,则有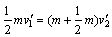
解得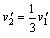 ⑤
⑤
A、C碰后上升高度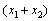 时,木块B刚好离开地面,此过程中,由机械能守恒定律有
时,木块B刚好离开地面,此过程中,由机械能守恒定律有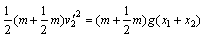 ⑥
⑥
由以上各式消去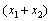 解得
解得