问题
计算题
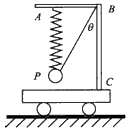
如图所示,在动力小车上固定一直角硬杆ABC,分别系在水平直杆AB两端的轻弹簧和细线将小球P悬吊起来,轻弹簧的劲度系数为k,小球P的质量为m,当小车沿水平地面以加速度a向右运动而达到稳定状态时,轻弹簧保持竖直,而细线与杆的竖直部分的夹角为θ,试求此时弹簧的形变量。
答案
解:设细线的拉力为T,则有
Tsinθ=ma,Tcosθ+F=mg,F=kx
联立解得:x=m(g-acotθ)/k
讨论:
(1)若a<g/cotθ,则弹簧伸长x=m(g-acotθ)/k
(2)若a=g/cotθ,则弹簧伸长x=0
(3)若a>g/cotθ,则弹簧压缩x=m(acotθ-g)/k
