问题
问答题
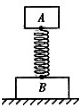
两木块A、B质量分别为m、M,用劲度系数为k的轻弹簧连在一起,放在水平地面上,如图所示,用外力将木块A压下一段距离静止,释放后A上下做简谐振动.在振动过程中,木块B刚好始终不离开地面(即它对地面最小压力为零).求:
(1)木块A的最大加速度;
(2)木块B对地面的最大压力大小;
(3)要使B离开地面,将A下压至静止的外力至少多大?
答案
(1)当弹簧处于伸长至最长状态时,M刚好对地面压力为零,
故弹簧中弹力F=Mg;此时m有最大加速度,
由F+mg=ma,得:
a=
.Mg+mg m
(2)由对称性,当m运动至最低点时,弹簧中弹力大小为F,但此时弹簧是处于压缩状态,
根据牛顿第二定律得:f-mg=ma
即f=m(g+a)=2mg+Mg
所以F压=f+Mg=2(m+M)g
(3)要使B离开地面,即当弹簧处于伸长至最长状态时,M刚好对地面压力为零时,F取最小值,
所以F≥ma=(m+M)g
即将A下压至静止的外力至少为(m+M)g
答:(1)木块A的最大加速度为am=
;(2)木块B对地面的最大压力大小为2(m+M)g;(3)要使B离开地面,将A下压至静止的外力至少为(m+M)g.Mg+mg m
