已知点列An(xn,0)满足:
(1)若xn+1=f(xn)(n∈N*),求f(x)的表达式; (2)已知点B(
(3)设(2)中的数列an的前n项和为Sn,试求:Sn<
|
(1)∵A0(-1,0),A1(1,0),∴
•A0An
=(xn+1)(xn+1-1),A1An+1
∴(xn+1)(xn+1-1)=a-1,∴xn+1=f(xn)=
,xn+a xn+1
∴f(x)=
.(3分)x+a x+1
(2)∵xn+1=f(xn)=
,a>1,∴xn>1,∴xn+1>2xn+a xn+1
∵
=(xn-BAn
,0),∴an=|BAn|=|x n-a
|.a
∵an+1=|x n+1-
|=|f(xn)-a
|=|a
-xn+a xn+1
|=a
•|xn-(
-1)a |xn+1|
|<a
(1 2
-1)•|xn-a
|=a
(1 2
-1)ana
∴要使an+1<an成立,只要
-1≤2,即1<a≤9a
∴a∈(1,9]为所求.(6分)
(3)∵an+1<
(1 2
-1)|xn-a
|<a
(1 22
-1)2•|x n-1-a
|<…<<a
(1 2n
-1)n•|x 1-a
|=a
(1 2n
-1)n+1,a
∴an<
(1 2n-1
-1)n(9分)a
∴Sn=a1+a2+…+an<(
-1)+a
(1 2
-1)2+…+a
(1 2n-1
-1)n=a (
-1)[1-(a
)n]
-1a 2 1-
(1 2
-1)a
(11分)
∵1<a≤9,∴0<
≤1,∴0<(
-1a 2
)n≤1(13分)
-1a 2
∴
<(
-1)[1-(a
)n]
-1a 2 1-
(1 2
-1)a
<
-1a 1-
(1 2
-1)a
-1a 1-(
-1)a
∴Sn<
(14分)
-1a 2- a

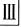 滞留,不松动。X线片示
滞留,不松动。X线片示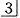 开窗牵引于牙区
开窗牵引于牙区