问题
问答题
如图所示,一个重为G的小球套在竖直放置的半径为R的光滑圆环上,一个劲度系数为k,自然长度为L(L<2R)的轻质弹簧,一端与小球相连,另一端固定在大环的最高点,求小球处于静止状态时,弹簧与竖直方向的夹角φ.
答案
以小球为研究对象,分析受力情况:竖直向下的重力G,弹簧的弹力F,圆环的弹力N,N沿半径方向背离圆心O,作出力图如图所示.
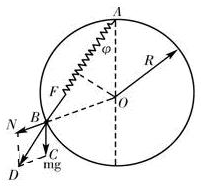
利用合成法,将重力G和弹力N合成,合力F合应与弹簧弹力F平衡.由图看出,力的三角形△BCD与△AOB相似,设AB长度为l,由三角形相似得:
=mg F
=. AO AB
,即得:F=R l mgl R
又由胡克定律有F=k(l-L),而l=2Rcosφ
联立上述各式可得:cosφ=kL 2(kR-G)
解得:φ=arccos
kL 2(kR-G)
答:小球处于静止状态时,弹簧与竖直方向的夹角为arccos
.kL 2(kR-G)
