问题
问答题
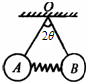
如图所示,A、B两球完全相同,质量均为m,用两根等长的细线悬挂在O点,两球之间固连着一根劲度系数为k的轻弹簧,静止不动时,弹簧位于水平方向,两根细线之间的夹角为2θ,已知下列各情况中,弹簧与AB两球心连线始终共线.求:
(1)系统静止时,弹簧的长度被压缩了多少?
(2)现在B上施加一水平向右的恒力,其大小为F,使得OA线竖直绷紧,求系统静止时弹簧的形变量;
(3)求上述(2)中OB线中张力的大小.
答案
(1)取B球受力分析可知:kx1=mgtanθ

解得x1=mgtanθ k
(2)当OA线处于竖直状态时,A球受到重力,竖直向上的拉力,弹簧中的弹力应为零.
所以有x2=0.
(3)小球受力如图所示:
由平行四边形定则可得:FT=(mg)2+F2
答:(1)系统静止时,弹簧的长度被压缩了x1=
;mgtanθ k
(2)系统静止时弹簧的形变量为零;
(3)上述(2)中OB线中张力的大小为FT=
.(mg)2+F2
