光滑平行的金属导轨MN和PQ间距L=1.0m,与水平面之间的夹角α=30°,匀强磁场磁感应强度B=2.0T,垂直于导轨平面向上,MP间接有阻值R=2.0Ω的电阻,其他电阻不计,质量m=2.0kg的金属杆ab垂直导轨放置,如下图所示,用恒力F沿导轨平面向上拉金属杆ab,由静止开始运动,v-t图象如下图所示,g取10m/s2,导轨足够长,求:
(1)恒力F的大小;
(2)金属杆速度为2.0m/s时的加速度大小;
(3)若从开始到达到最大速度过程中,流过R的电荷量为2C,则在这个过程里所发生的位移是多少?
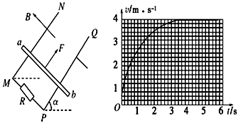
(1)由图知,在恒力F作用下金属杆ab达到的最大速度 vmax=4 m/s,此时杆做匀速直线运动,则有
F-mgsin α-F安=0
又感应电流 I=BLvm R
安培力大小为F安=
,B2L2vm R
联立得 F=mgsinα+
,B2L2vm R
代入解得 F=18 N.
(2)由牛顿第二定律得:
F-mgsin α-F安′=ma
将v=2 m/s时,F安′=B2L2v R
根据牛顿第二定律得
a=F-mgsinα- B2L2v R m
代入解得,a=2m/s2.
(3)由法拉第电磁感应定律得:E=
=△φ △t
①B△S △t
而 q=I△t=
②E△t R
由①②式得:q=
且△S=L•xB△S R
所以:x=2m
答:
(1)恒力F的大小是18N;
(2)金属杆速度为2.0m/s时的加速度大小是2m/s2;
(3)若从开始到达到最大速度过程中,流过R的电荷量为2C,则在这个过程里所发生的位移是2m.
