问题
问答题
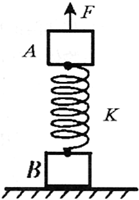
一个劲度系数为K=800N/m的轻弹簧,两端分别连接着质量均为m=12kg物体A和B,将它们竖直静止地放在水平地面上,如图所示.施加一竖直向上的变力F在物体A上,使物体A从静止开始向上做匀加速运动,当t=0.4s时物体B刚离开地面(设整个匀加速过程弹簧都处于弹性限度内,取g=10m/s2).求:
(1)此过程中物体A的加速度的大小
(2)此过程中所加外力F所做的功.
答案
(1)开始时弹簧被压缩X1,对A:KX1=mAg ①
B刚要离开地面时弹簧伸长X2,对B:KX2=mBg ②
又mA=mB=m代入①②得:X1=X2
整个过程A上升:S+X1+X2=
=0.3m2mg k
根据运动学公式:S=
at21 2
解得物体A的加速度:a=
=3.75m/s22S t2
(2)设A末速度为Vt 则由:S=
得:vt=v0+vt 2
=1.5m/s2S t
∵X1=X2∴此过程初、末位置弹簧的弹性势能不变,弹簧的弹力做功为零.设此过程中所加外力F做功为W,根据动能定理:
W-mgS=
mvt21 2
解得:W=49.5J
答:(1)此过程中物体A的加速度的大小为3.75m/s2;
(2)此过程中所加外力F所做的功为49.5J.
