问题
问答题
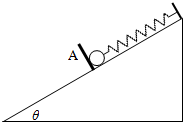
如图所示,一轻质弹簧的一端固定于倾角为θ的光滑斜面上端,另一端系一质量为m的小球,小球被一垂直于斜面的挡板A 挡住,此时弹簧恰好为自然长度.现使挡板A以恒定加速度a(a<gsinθ)匀加速沿斜面向下运动(斜面足够长),已知弹簧的劲度系数为k.
(1)求小球开始运动时挡板A对小球提供的弹力;
(2)求小球从开始运动到与档板分离弹簧的伸长量;
(3)问小球与档板分离后能否回到出发点?请简述理由.
答案
(1)设小球受挡板的作用大小为N,刚开始时,弹簧为自然长度,对小球无作用力.
由牛顿第二定律,得
mgsinθ-N=ma,
得 N=mgsinθ-ma
(2)小球与档板分离时弹力N=0,有 mgsinθ-F=ma,
得 F=mgsinθ-ma
由胡克定律得弹簧的伸长量 △x=
=F k mgsinθ-ma k
(3)小球再能回到出发点是不可能的.因为若小球再能回到出发点,则对于整个运动过程来说,由于挡板做负功而机械能减小,这将出现矛盾.
答:( 1 )小球刚开始运动时挡板对小球提供的弹力大小F=mgsinθ-ma.
(2)小球从开始运动到与档板分离弹簧的伸长量为
.mgsinθ-ma k
(3)小球再能回到出发点是不可能的.因为若小球再能回到出发点,则对于整个运动过程来说,由于挡板做负功而机械能减小,这将出现矛盾.
