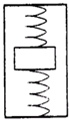
两个质量不计的弹簧将一金属块支在箱子的上顶板与下底板之间,箱只能沿竖直方向运动,如图所示.两弹簧原长均为0.80m,劲度系数均为60N/m.当箱以a=2.0m/s2的加速度匀减速上升时,上弹簧的长度为0.70m,下弹簧的长度为0.60m.(g=10m/s2)若上顶板压力是下底板压力的四分之一,试判断箱的运动情况.
根据胡克定律F=Kx,设下弹簧压力为N1、上弹簧压力为N2
N1=60×(0.80-0.60)=12.0N
N2=60×(0.80-0.70)=6.0N,
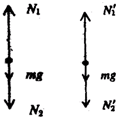
以向下为正方向,当金属块以2.0m/s2的加速度匀减速上升时,金属块受力如图:
由牛顿第二定律:mg+N2-N1=ma
10m+6-12=2m∴m=0.75Kg
弹簧总长度不变:l总=l1+l2=0.70+0.60=1.30m,
上顶板压力为下底板压力的
时,1 4
设上弹簧的压缩量为X
、下弹簧压量为X ′2
, ′1
则X
=4X ′1
,2l0-5X ′2
=l总 ′2
算出X
=0.60mN ′2
=KX ′2
=60×0.06=3.6N ′2
N
=4N ′1
=4×3.6=14.4N ′2
mg+N
-N ′2
=ma′ ′1
5+3.6-14.4=0.75a′
得a′=4.4m/s2
箱子以大小为4.4m./s2的加速度加速上升
或减速下降
答:箱子以大小为4.4m./s2的加速度加速上升或减速下降.
